Introduction to our FHE compiler
Using fully homomorphic encryption (FHE), anyone can perform computations directly on private (i.e. encrypted) data, without ever having to decrypt it. FHE has the power to improve how we interact with existing applications and enable entirely new applications—from allowing sophisticated parties to protect their trading strategies while trading on blockchains (i.e. hidden trading strategies) to fine-tuning advanced machine learning models over sensitive data sets (e.g. customized AI agents).
However, using the technology today is really difficult for a non-expert.
Our next-generation compiler is designed to make it easy for any engineer to write highly optimized FHE programs (benchmarks available here). Instead of rewriting an application in some niche eDSL, our vision is that engineers should bring their existing program written in a mainstream language and simply add directives to indicate which functions are FHE programs and which inputs/outputs should be kept hidden! If you’re familiar with RiscZero or Succinct, we’d say our approach is closest in spirit to theirs (though we focus on FHE rather than ZK).
Initially, we support C. Depending on demand, we may add support for Rust as well.
Brief intro to FHE
FHE is the next generation of public key cryptography. In addition to being able to encrypt and decrypt data, we can now perform arithmetic, logical, and comparison operations directly over the encrypted data without ever decrypting said data. This means we can process data for purposes such as order book matching in financial systems or ML inference while protecting the user data going into these systems.
FHE relies on a special type of cryptography called lattice based cryptography.
Certain variants of FHE, such as threshold FHE (which we won’t go into here), enable running arbitrary computer programs over multiple users’ private data. Users can thus protect their data while still allowing it to be used in an application.
You may wonder how FHE differs from other privacy-preserving technologies. Briefly, some nice things about FHE include:
- The computation itself is non-interactive, so it’s great for decentralized settings where parties may be in very different locations around the world.
- FHE is resistant to many attacks, e.g. FHE is not susceptible to the broad range of attacks trusted execution environments (TEEs) are susceptible to.
- FHE is post-quantum, meaning FHE is secure against attacks from a quantum computer. An alternative way of thinking about this property is that FHE is “future-proof” even when ciphertexts are stored by an adversary for the day when quantum computers are available.
How Parasol differs from our first-generation compiler
If you worked with our first-generation FHE compiler, you may wonder how our new one differs.
Some important changes to call out include:
- Moving away from an eDSL approach. Now developers write directly in a mainstream language.
- Moving from the BFV scheme to our own variant of Torus FHE (TFHE). This allows us to support comparison operations more easily and cheaply.
- Unlimited computation over encrypted data. Previously, we could only support running a limited number of operations on encrypted data.
- Program composability. Previously, a developer could create different programs using our compiler and these programs would not automatically be compatible with one another. Programs generated using our new compiler no longer have this issue.
Some hardcore technical details about our approach
Feel free to skip this! You don’t need to understand these details to work with our tools.
The full stack
Listed in order of top layer to bottom layer, Parasol consists of:
LLVM-based compiler: What developers interact with to write and compile their FHE programs.
Virtual processor: Efficiently runs what’s output by the compiler. We have our own instruction set (ISA); we may consider switching to RISC-V in the future.
FHE library: Implements low-level cryptographic operations in our variant of the TFHE scheme.
How things fit together
We build an LLVM-based compiler to provide a great developer experience. This approach has two benefits. First, it allows developers to use a variety of mainstream programming languages like Rust, C, or C++, with the only changes to their programs being the directives mentioned above. Second, it allows us to leverage decades of optimizations and transformations that are already built into LLVM.
Building the Parasol compiler was very technically challenging and required designing and implementing a virtual processor that operates over a mix of plaintext and encrypted data (aka the parasol processor). The processor is integrated as a backend for the LLVM toolchain, which requires us to map our instruction set architecture to the internal LLVM representations. We adopt an out-of-order processor design and feature dynamic scheduling within instructions to maximize parallelism.
Our compiler and processor rely on an in-house created variant of the TFHE scheme. We chose TFHE as it gives developers access to a variety of operations—most importantly, comparisons. A key feature of FHE is “bootstrapping” which is an operation to reduce noise in ciphertexts, allowing us to compute indefinitely. It tends to be a relatively expensive operation to perform, and there are various flavors of bootstrapping for the TFHE scheme.
What’s special about our TFHE variant is that it utilizes circuit bootstrapping and (homomorphic) multiplexer trees to realize arbitrary computation. This form of bootstrapping, if configured correctly, allows us to extract and maximize parallelism in programs. In taking this approach, we rely on a cheap multiplexer operation to do data propagation. In contrast, when working with functional/programmable bootstrapping, data propagation is instead achieved through the much more expensive bootstrap operation. If you’d like to learn more about this, feel free to jump here.
The benefits of our approach may not be obvious on laptops or smaller machines but maximizing parallelism will be key to unlocking FHE’s performance promise over the coming years. Note that in running programs locally you will not experience much, if any, performance advantage from our tech as you need dozens of cores.
Preliminary knowledge
To effectively use our compiler, we assume some basic knowledge of cryptography along with C and Rust.
Cryptography
- Plaintext vs. ciphertext: Plaintext refers to unencrypted data (i.e. data in the clear) whereas ciphertext refers to encrypted data.
- Public key vs. private key: In public key cryptography, there are two types of keys. The public key (aka the encryption key) can be shared with others. Using the public key, people can send encrypted messages. The private key (aka the decryption key) should not be shared. Whoever holds the private key can decrypt the messages addressed to them (which are encrypted under the corresponding public key). Usually, each person has their own public/private key pair.
- “Homomorphic”: We use this term to denote computations performed directly on encrypted data. For example, if we say “homomorphic addition,” we are referring to addition of ciphertexts. What’s magical about FHE is that computations performed over the ciphertexts corresponds to computations performed over the plaintexts.
FHE computing model
In FHE, we assume there are a few different parties. We have the data owner with a public-private key pair and we have a separate computing party who has access to powerful hardware. The computing party is responsible for performing the computations over the encrypted data and sending the encrypted result back to the data owner. At no point in time can the computing party see the data in the clear.
Thus, in addition to to the public and private key, we have a special key that we call the “compute key.”
The compute key will be used by whoever is performing the FHE computation over the encrypted data. If you’ve worked with other FHE libraries, this is sometimes called the server key or evaluation key.
In theory, we could group this together with the public key, as the compute key only enables computation and not decryption. We have chosen not to do this as the compute key is orders of magnitude larger than the public key.
C, Rust, and programming
As FHE programs are currently written in C, you should be familiar with C basics like pointers, integer types, and casting rules. You should also be familiar with basic C programming patterns such as output parameters.
As our processor is written in Rust, you will also need to be familiar with basic Rust constructs to interact with and test the programs themselves.
Who should use our compiler?
If you’re building an application that operates on user data but want to ensure all user inputs remain private, you’ve come to the right place!
Parasol was designed to be used by any engineer—allowing you to write your FHE program in a standard programming language like C. No need to learn an eDSL or a newly created language.
You’re a web3 engineer.
We have a special offering in store for web3 engineers :)
Feel free to experiment with Parasol which forms the basis of Sunscreen’s secure processing framework (aka the SPF).
SPF will allow you to easily create, deploy, and use (threshold) FHE applications on any chain, regardless of virtual machine. We’ll also help you manage access control and data storage.
You’re a web2 engineer.
Performance is very important to you but you don’t have the time to learn about FHE or a new eDSL.
We enable you to work with a familiar programming language, only adding directives to your program to indicate which functions are FHE programs and which arguments are encrypted.
You’ll also have access to a variety of operations like arithmetic, logical, and comparison operations.
If you’re primarily wanting to do arithmetic heavy applications like matrix-vector multiplication, we would recommend working with the CKKS scheme for now as it provides better performance for these operations.
You’re a researcher.
You want to quickly prototype FHE applications without fussing over parameters or circuits. However, performance is very important and you don’t want to introduce a significant slowdown by working with an FHE compiler (over working with the FHE scheme directly).
Getting started
This chapter walks through how to get started using our FHE compiler.
Installation
To use the Parasol compiler, you will need to download our variant of clang that supports the Parasol processor target. You can download the latest version for your platform from our github repo.
These tarballs contain the clang, ld.lld, and llvm-objdump binaries. Place these binary in your PATH environment variable to be able to call then, or specify the full path when executing the specific programs.
If you would like to run the executables generated by the compiler, you will need to have Rust installed. We recommend using rustup to install Rust.
Important to note
This is an early version of our TFHE compiler and has limited functionality. Importantly, please note that:
- Branching directly over encrypted data is not supported. To see what is supported today, please see here.
- Our technology shines if programs are run on a machine with sufficient computing resources; a rough heuristic is you want to run the program on a machine that has at least as many cores as input bits (e.g. if you want to add two 16-bit integers together, you need ~32 cores).
My first FHE program
Now that we have installed the Sunscreen crate as a dependency, let’s get started writing our first private app using FHE! Writing our program will be a gradual process and we’ll add more code as we progress through this section. In this example, we will be developing a program to add two encrypted integers using the following C program.
Writing our program
// fhe-programs/src/add.c
typedef unsigned char uint8_t;
[[clang::fhe_program]] uint8_t add([[clang::encrypted]] uint8_t a,
[[clang::encrypted]] uint8_t b) {
return a + b;
}
Notice that the add function is similar to any other function in C, except for the attributes. This is where the magic happens—these attributes define which functions should be compiled into FHE programs (using [[clang::fhe_program]]) and which inputs are encrypted values (using [[clang::encrypted]]).
add’s signature specifies both the unsigned uint8_t values being added and that the returned value is another uint8_t value. The [[clang::encrypted]] attribute tells the compiler to treat that specific value as a ciphertext instead of a plaintext value when the program is run.
One final important note on the add program is that libraries can be included using the #include directive, just an in normal C. To use these functions inside a FHE function (one marked with [[clang::fhe_program]]), the function must be marked as inline.
Compiling our program
Now that we have our add program, we can compile it using the Sunscreen version of clang that supports the Parasol processor.
# Create the object file
clang \
-target parasol \ # Target the parasol CPU
-O2 \ # Turn on compiler optimizatons
-c \ # Only run compile, do not link
add.c \ # Specify the file to compile
-o add.o # And where to write the output
# Combine object files into a single binary
ld.lld \
add.o \ # Specify the file to link
-o add # And where to write the output binary file
This will produce a small binary file at fhe-programs/compiled/add. This file is an Executable and Linkable Format (ELF) file that contains some metadata about the Parasol programs, the specific FHE programs specified with [[clang::fhe_program]], and the assembly code to run the FHE programs on the Parasol processor.
Great, we now have the file! But uh, how do we actually run a program over encrypted data? Luckily the code to run a FHE program on the Parasol processor is easy to write in Rust. We will walk through the following example.
Running the program
use parasol_cpu::{run_program, ArgsBuilder};
use parasol_runtime::{
fluent::UInt8, ComputeKey, Encryption, SecretKey,
};
const FHE_FILE: &[u8] =
include_bytes!("../fhe-programs/compiled/add");
fn main() {
// Generate a secret key for the user. By default this ensures
// 128 bit security.
let secret_key =
SecretKey::generate_with_default_params();
// Generate a compute key for the user. These keys are used for
// operations and do not give access to the plaintext data;
// therefore, this key can safely be shared with another party.
let compute_key =
ComputeKey::generate_with_default_params(
&secret_key,
);
// Get the default encryption parameters.
let enc = Encryption::default();
// Define the values we want to add. The sizes of the values
// must match the size of the values defined in the
// C TFHE program!
let a = 2u8;
let b = 7u8;
let enc_a =
UInt8::encrypt_secret(a as u64, &enc, &secret_key);
let enc_b =
UInt8::encrypt_secret(b as u64, &enc, &secret_key);
// To pass arguments into the C program, we must use
// the `ArgsBuilder` to construct the arguments.
let arguments = ArgsBuilder::new()
.arg(enc_a)
.arg(enc_b)
.return_value::<UInt8>();
// Run the program.
let encrypted_result = run_program(
compute_key,
FHE_FILE,
"add",
arguments,
)
.unwrap();
// Decrypt the result.
let result =
encrypted_result.decrypt(&enc, &secret_key);
println!("Encrypted {a} + {b} = {result}");
}First, we must generate a secret key. This key allows the user to both encrypt and, crucially, decrypt data that has been processed by an FHE program.1 As such, this key should be kept secret (hence the name!) in order to prevent others from decrypting the result of an FHE program.
We then generate the compute key which allows anyone to run FHE programs on data that was encrypted using the secret key, such as our add program. Crucially this key only allows for processing of encrypted data to produce new encrypted data, and does not provide the ability to decrypt the data at any point during or after an FHE program has been executed. This key can be shared with a service with large compute resources in order to evaluate a program more quickly.
After generating all the keys, we are ready to start! The first step is to encrypt the values using our secret key. For this we use the UIntN::encrypt_secret method, which specifies that we want to generate an encrypted value of size N bits. This provides us with the encrypted values enc_a and enc_b.
These encrypted values can they be passed as arguments via the definition of arguments, which uses the builder pattern to specify the inputs to the program. Arguments are specified with the args method, which in this case are enc_a and enc_b. The return value is specified using the return_value method, here specified to be a UInt8 value. Calling return_value converts the ArgsBuilder into an Args, which is the bundled up arguments that can be passed to the program.
We finally get to the good stuff—running the program. Here we simply call run_program with our compute key, the generated add ELF file, the name of the specific program to run (in this case add), and the encrypted arguments. This function returns the encrypted value.
We can now decrypt the result of our program using the decrypt method, which takes in the encryption parameters and the secret key. This returns a regular unsigned integer value, which we print to the console.
Congrats! You have successfully written and executed your first FHE program. 🎉
We also support public key encryption (so that we would have a secret key, public key, and compute key). For simplicity, this example uses the secret key for both encryption and decryption instead.
Properties of a FHE Program
Current state-of-the-art in FHE (including our work) enables unbounded computation, meaning programs of arbitrary length can be executed.
We support many common operations such as addition, multiplication, and comparison. There are some restrictions on what can be expressed due to the encrypted nature of the computation. This section will go over these basics as well as inherent limitations of FHE programs.
What does our compiler offer?
Our compiler abstracts away the usual difficulties of working with FHE which includes selecting FHE scheme parameters, translating your program into an optimized circuit representation, and inserting in FHE-specific operations.
We have currently configured Parasol to provide 128 bits of security (estimated via Lattice Estimator).
Additionally, our compiler plugs into our single-key TFHE scheme variant (useful if your application operates over a single user or entity’s data) as well as our threshold TFHE scheme variant (useful if your application operates over data from multiple users or entities).
While this list isn’t comprehensive, these are the main features we’d like to call attention to:
- Support for C programs
- Signed and unsigned integers up to 32 bits
- Arithmetic, logical, and comparison operations
- Array support
- Branching over plaintext values
- Support for import statements (
#include) - Support for function inlining, enabling more modular code
- Ability to perform computations on combinations of plaintexts and ciphertexts (e.g. you can multiply a ciphertext and plaintext together to produce a new ciphertext)
- Run computations without FHE (useful for testing purposes)
- Programs are automatically optimized and program execution is automatically parallelized
- Support for serialization of keys and ciphertext values
Upcoming features
- Higher precision integers
- Division by plaintext
- Branching over encrypted values (with the usual FHE restrictions such as evaluating both conditions for an if statement, cannot exit a loop early, etc.)
- WASM support (some support is available today)
Functions and Types
Types and type conversions
Programs written for the Parasol CPU currently supports signed and unsigned integers up to 32 bits. You can use the following types, which are synonyms for the corresponding types in the C standard library:
// Boolean value
typedef _Bool bool;
// 8 bit unsigned integer
typedef unsigned char uint8_t;
// 16 bit unsigned integer
typedef unsigned short uint16_t;
// 32 bit unsigned integer
typedef unsigned int uint32_t;
// 8 bit signed integer
typedef signed char int8_t;
// 16 bit signed integer
typedef signed short int16_t;
// 32 bit signed integer
typedef signed int int32_t;
When a program is running, it is possible to convert between different integer sizes. When converting from a smaller integer to a larger one, the higher bits are padded and therefore the value does not change. However, when converting from a larger integer to a smaller one, the higher bits are discarded, leading to a different value.
Here is an example:
[[clang::fhe_program]] void size_conversions(
[[clang::encrypted]] uint8_t u8_a,
[[clang::encrypted]] uint32_t u32_b,
[[clang::encrypted]] uint32_t *u32_output,
[[clang::encrypted]] uint8_t *u8_output
) {
// Convert to a larger integer
uint32_t u32_a = u8_a;
*u32_output = u32_a + u32_b;
// Truncate to a smaller integer
char u8_b = u32_b;
*u8_output = u8_a + u8_b;
}
Function parameter annotations
FHE programs can be run with either plaintext or ciphertext arguments. In order to specify what argument is of what type, you can use the [[clang::encrypted]] annotation before a function’s parameter.
[[clang::fhe_program]] uint32_t f(
uint32_t a,
[[clang::encrypted]] uint32_t b
) {
// do something with a and b
}
In this particular example function, the first parameter is expected to be a plaintext value, while the second parameter is expected to be an encrypted value. When the program is run, the parameters passed to the function should match the annotation given at the time of compilation.
Return parameters
One can specify a return value (signed or unsigned integer) by using the standard C return type syntax.
// Function to return a value
[[clang::fhe_program]] uint32_t add(
[[clang::encrypted]] uint32_t a,
[[clang::encrypted]] uint32_t b
) {
return a + b;
}
We can also return values by modifying the arguments. Here we take two numbers, add them together, and store the result in the second parameter. This overwrites the value in the memory location pointed to by the balance_pointer parameter.
The fact that you can overwrite a pointer is important. Here is an example of a private transfer function:
[[clang::fhe_program]] void transfer(
[[clang::encrypted]] uint32_t amount,
[[clang::encrypted]] uint32_t *balance_pointer
) {
uint32_t balance = *balance_pointer;
uint32_t transfer_amount = amount < balance ? amount : 0;
*balance_pointer = balance - transfer_amount;
}
In this example, the balance_pointer takes in the orignal balance and after the transfer program has run, that same argument is updated with the new balance.
Inlining
One of the tenets of making maintainable code is developing smaller functions that can be reused in several places, increasing the readability of a program. For our FHE programs, functions marked as inline can be used to reduce common/boilerplate code in the program, making the final code easier to reason about and test.
The following example demonstrates this modularity. It is a program that calculates the price of some item given its base price and a packed byte representing the discounts a user could have applied to their purchase. The get_bit function is used several times to extract the specific discounts from the discounts_flags argument. These discounts are then used to calculate the final price of the item. Inlining here enables us to follow DRY principles and reduce code duplication.
inline bool get_bit(uint32_t flags, unsigned int n) {
return ((flags >> n) & 0x1);
}
[[clang::fhe_program]] uint32_t price_item(
uint32_t base_price,
[[clang::encrypted]] uint32_t discounts_flags
) {
bool has_store_membership_discount = get_bit(discounts_flags, 0);
bool has_coupon_discount = get_bit(discounts_flags, 1);
uint32_t price = base_price;
// Discount the items based on the discounts the customer has
price = has_store_membership_discount ? price - 2 : price;
price = has_coupon_discount ? price - 3 : price;
return price;
}
Comparisons, Branching, and Loops
Programs are often written with control flow structures such as conditionals and loops in order to repeat actions or change the flow of execution based on certain conditions. Here will will go into what control flow mechanisms can be expressed in a FHE program.
Comparisons
We support the common comparison operators between plaintext and encrypted values: <, >, <=, >=, ==, and !=.
[[clang::fhe_program]] void compare(
[[clang::encrypted]] uint32_t a,
[[clang::encrypted]] uint32_t b,
[[clang::encrypted]] bool *result_lt,
[[clang::encrypted]] bool *result_gt,
[[clang::encrypted]] bool *result_le,
[[clang::encrypted]] bool *result_ge,
[[clang::encrypted]] bool *result_eq,
[[clang::encrypted]] bool *result_ne
) {
*result_lt = (a < b);
*result_gt = (a > b);
*result_le = (a <= b);
*result_ge = (a >= b);
*result_eq = (a == b);
*result_ne = (a != b);
}
Branching and the Ternary Operator
We do not support if statements in FHE programs at the moment. However, we do support the ternary operator ?: which can be used to implement choosing between two values based on a condition. This enables writing more complex logic in FHE programs.
[[clang::fhe_program]] uint8_t max(
[[clang::encrypted]] uint8_t a,
[[clang::encrypted]] uint8_t b
) {
// Use the ternary operator to select the maximum value
return (a > b) ? a : b;
}
Loops
Loops where the loop condition is in plaintext are supported in FHE programs, which includes both while loops and for loops.
[[clang::fhe_program]] uint32_t sum(
[[clang::encrypted]] uint32_t* a,
uint32_t len
) {
uint32_t x = 0;
for (uint32_t i = 0; i < len; i++) {
x += a[i];
}
return x;
}
Deploying a FHE program
We now look at how to compile and run FHE programs.
Compiling FHE programs
Say we had the following FHE program:
typedef unsigned char uint8_t;
[[clang::fhe_program]] uint8_t add([[clang::encrypted]] uint8_t a,
[[clang::encrypted]] uint8_t b) {
return a + b;
}
If we wanted to compile this program, we can use the Sunscreen version of clang that supports the Parasol processor using the following command:
# Create the object file
clang \
-target parasol \ # Target the parasol CPU
-O2 \ # Turn on compiler optimizatons
-c \ # Only run compile, do not link
add.c \ # Specify the file to compile
-o add.o # And where to write the output
# Combine object files into a single binary
ld.lld \
add.o \ # Specify the file to link
-o add # And where to write the output binary file
This will produce a small binary file at add. This file is an Executable and Linkable Format (ELF) file that contains some metadata about the Parasol programs, the specific FHE programs specified with [[clang::fhe_program]], and the assembly code to run the FHE programs on the Parasol processor.
The file generated here can be used with SPF to execute the program. For more information, see my first program
Running FHE programs
As seen in the previous sections, we can write FHE programs using the Sunscreen compiler. Now that we have our program compiled into an ELF file, we can run it on the Parasol processor by writing a small Rust program that uses SPF to execute the program.
Rust programs in general are structured as so; we will go through the steps in turn.
#![allow(unused)] fn main() { // Generate a secret key for the user. By default this ensures // 128 bit security. let secret_key = SecretKey::generate_with_default_params(); // Generate a compute key for the user. These keys are used for // operations and do not give access to the plaintext data; // therefore, this key can safely be shared with another party. let compute_key = ComputeKey::generate_with_default_params( &secret_key, ); // Get the default encryption and evaluation parameters. let enc = Encryption::default(); let eval = Evaluation::with_default_params(&compute_key); // To pass arguments into the TFHE C program, we must use // the `ArgsBuilder` to specify the arguments. let arguments = ArgsBuilder::new() .arg(UInt8::encrypt_secret(5, &enc, &secret_key)) .arg(UInt8::encrypt_secret(10, &enc, &secret_key)) //... .return_value::<UInt8>(); // Allocate memory for the FHE program to run on, as well as a pointer to the // specific function to execute. let memory = Arc::new(Memory::new_from_elf(&fhe_file)?); let program = memory.get_function_entry("FUNCTION_NAME")?; // Generate the FHE computer instance that will run the program. let computer = FheComputer::new( &enc, &eval ); // Run the programs let encrypted_result = computer.run_program( &program, memory, arguments, )?; // Decrypt the result. let result = encrypted_result.decrypt(&enc, &secret_key); }
Keys
When running a program, we need to generate two types of keys:
- Secret key: This key is used to encrypt and decrypt data. It should be kept secret as it allows the user to decrypt the results of FHE programs.
- Compute key: This key is used to run FHE programs on encrypted data. It does not allow decryption of the data, so it can be shared with a computing party that will run the FHE programs.
For simplicity, we assume the encryption key and decryption key are the same. If desired, a public/secret key pair could instead be generated so that the encryption and decryption key are different.
Argument builder
The ArgsBuilder is used to specify the arguments to the FHE program.
Arguments are specified with the arg method, which can be called multiple times to add multiple arguments. These arguments can be either plaintext values or encrypted values, including pointers (see “Memory” below). These values will need to be the same integer sizes as what is specified in the C program.
The return value of the program is specified using either the return_value::<type>() method, or if there is no return value, then no_return_value() can be used. This converts the ArgsBuilder into an Args, which is the bundled up arguments that can be passed to the program.
Memory
You can also pass in pointers to memory locations that will be used by the FHE program. To do this you will need to create an FheComputer instance and allocate memory for the program to use. The memory can be allocated from an ELF file, which contains the compiled FHE program.
// Initialize the memory space, specifying which ELF file to use.
let memory = Arc::new(Memory::new_from_elf(fhe_file))?);
// Create array of 8 elements of 16-bit unsigned integers.
let data = std::array::from_fn::<_, 8, _>(
|i| UInt16::encrypt_secret(i as u64, &enc, &secret_key)
);
// Allocate memory for `data` in the FHE memory space.
let data_ptr = memory.try_allocate_type(&data)?;
// Now use the `data_ptr` in the `ArgsBuilder` as an argument to the FHE program.You can also allocate an array of memory that is uninitialized, which will be filled in by the FHE program. This is useful when you want to run a program that produces multiple outputs or to pass a scratch buffer into your program.
// Instead of specifying a value, specify empty memory locations that will be
// filled in by the FHE program.
let data_buffer = std::array::from_fn::<_, 2, _>(|_| UInt16::new(&enc));
let data_buffer_ptr = memory.try_allocate_type(&data_buffer).unwrap();
// Now use the `data_buffer_ptr` in the `ArgsBuilder` as an argument to the FHE program.Running the program
Once you have your Args and Memory set up, you can run the program using the FheComputer instance. The run_program method takes in the program to run, the memory to use, and the arguments to pass in. It returns an encrypted result (if applicable) that can be decrypted using the secret key.
let encrypted_result = computer.run_program(
&program,
memory,
arguments,
)?;Testing the program with plaintext values
When testing your FHE programs, you may want to run them with plaintext values instead of encrypted values to ensure that the logic is correct. You can do this by passing in all plaintext values to the ArgsBuilder and then calling run_program. This will run the program without FHE, allowing you to test the logic of your program without the overhead of encryption and decryption.
let first_value = 5u8;
let second_value = 10i8;
// ... plus all other values you want to pass in
// Encrypted version of the arguments
let encrypted_arguments = ArgsBuilder::new()
.arg(UInt8::encrypt_secret(first_value, &enc, &secret_key))
.arg(Int8::encrypt_secret(second_value, &enc, &secret_key))
//... other unsigned or signed values
.return_value::<UInt8>();
// Plaintext arguments, useful for debugging or testing
let plaintext_arguments = ArgsBuilder::new()
.arg(first_value)
.arg(second_value)
//... other unsigned or signed values
.return_value::<u8>();Decrypting the result
After running the program, you will receive an encrypted result. To decrypt this result, you can use the decrypt method on the encrypted value, passing in the encryption parameters and the secret key.
let result = encrypted_result.decrypt(&enc, &secret_key);You can also decrypt memory values that were allocated in the FHE memory space. This is useful when you have run a program that produces multiple outputs or modifies data in place.
// Get a [UInt16; 8] array from the memory space that you can decrypt
let data_buffer_encrypted = memory.try_load_type::<[UInt16; 8]>(data_buffer_ptr)?;Applications
In this section, we’ll walk through some relatively simple but still interesting applications of FHE.
Private transaction
Private transactions are very useful in the context of blockchain as they allow you to send a hidden amount of currency to someone else.
In this paradigm, your account balance, the recipient’s account balance, and the transfer amount are all hidden (i.e. encrypted). This prevents other parties from knowing how much money you have or how much money you’re sending another party.
Please note that to properly implement a private transaction on an actual blockchain, you would want to use threshold FHE rather than single-key FHE. This experience is possible via our SPF offering :)
How will our algorithm work?
The transfer algorithm works quite simply; it adds the transfer amount to the recipient’s balance and subtracts it from the sender’s balance. There are however two potential issues that need to be addressed:
- Underflow: If the sender does not have enough funds to perform the transfer, the transfer should not be performed.
- Overflow: If adding the transfer amount to the recipient’s balance would cause it to overflow, the transfer should not be performed. For example, if the recipient’s balance is
UINT32_MAXand the transfer amount is1, the recipient’s balance would overflow to0, which should not be allowed.
To check for these issues, we use the ternary operator ? : to conditionally set the transfer amount to zero if the sender does not have enough funds to perform the transfer or if the transfer would cause the recipient’s balance to overflow. Even if the transfer amount ends up being zero, two new ciphertexts for the balances will be generated, ensuring that the result of the transfer is kept private.
“Normal” program (aka no privacy)
Here is plaintext version of the program, where neither the sender not the recipient has privacy for the transaction.
void transfer(uint32_t *sender_balance_pointer,
uint32_t *recipient_balance_pointer,
uint32_t transfer_amount) {
uint32_t sender_balance = *sender_balance_pointer;
uint32_t recipient_balance = *recipient_balance_pointer;
// Conditions that need to be met for a transfer to be valid
bool sender_can_transfer = transfer_amount <= sender_balance;
bool recipient_can_receive =
recipient_balance + transfer_amount >= recipient_balance;
// Determine the fundable transfer amount
uint32_t fundable_transfer_amount =
(sender_can_transfer && recipient_can_receive) ? transfer_amount : 0;
// Update the balances
*sender_balance_pointer = sender_balance - fundable_transfer_amount;
*recipient_balance_pointer = recipient_balance + fundable_transfer_amount;
}
We define the function that takes in the balances and transfer amount via transfer. In this code we will be updating the balance values in-place through their pointers; for FHE programs, all inputs are required to be passed in by reference and hence the plaintext version follows this convention.
We check if the sender has enough funds to perform the transfer (sender_can_transfer) and if the transfer would cause the recipient’s balance to overflow (recipient_can_receive), handling the two edge cases mentioned earlier.
If the sender is able to transfer the funds and the receiver is able to receive them, we keep the transfer amount specified. Otherwise, we set the transfer amount to zero to prevent any transfer from occurring. This can be seen in fundable_transfer_amount. Finally, we update the balances!
Private program walkthrough
To transform the above program into one providing privacy for both the sender and receiver, we include [[clang:fhe_program]] for the transfer function so that our compiler knows that this should be transformed into an FHE program operating on private data.
To indicate that the sender’s balance, recipient’s balance, and transfer amount should be hidden from others view, we include [[clang:encrypted]]].
And that’s it, you now have an FHE program where only the sender and recipient know the transfer amount!
[[clang::fhe_program]]
void transfer([[clang::encrypted]] uint32_t *sender_balance_pointer,
[[clang::encrypted]] uint32_t *recipient_balance_pointer,
[[clang::encrypted]] uint32_t transfer_amount) {
uint32_t sender_balance = *sender_balance_pointer;
uint32_t recipient_balance = *recipient_balance_pointer;
// Conditions that need to be met for a transfer to be valid
bool sender_can_transfer = transfer_amount <= sender_balance;
bool recipient_can_receive =
recipient_balance + transfer_amount >= recipient_balance;
// Determine the fundable transfer amount
uint32_t fundable_transfer_amount =
(sender_can_transfer && recipient_can_receive) ? transfer_amount : 0;
// Update the balances
*sender_balance_pointer = sender_balance - fundable_transfer_amount;
*recipient_balance_pointer = recipient_balance + fundable_transfer_amount;
}
Running the program
If you’d like to run the program, feel free to look at the corresponding code here.
Performance
Running the program takes 0.327 seconds on an AWS c7a.16xlarge machine [64 cores] and 1.28 seconds on an 14 inch M2 Macbook Pro with 10 cores (6 performance, 4 efficiency).
What’s missing?
For simplicity, we’ve omitted details that are needed to properly execute a private transaction in real life, such as where to store the encrypted values and providing a private funding method for the accounts.
First-price sealed-bid auction
Auctions are core to trading (e.g. treasury auctions, order flow auctions) and can be thought of as the building block for how most centralized exchanges operate today. In this example, we consider a first-price sealed-bid auction over encrypted bids.
How will our algorithm work?
Our program finds the highest bid amount and who placed the highest bid in a sealed-bid auction. The algorithm takes the first bid in the list and marks it as the winning bid. Then, subsequent bids are compared to this winning bid in turn using a for loop. If a higher bid is found, it replaces the current winner. Finally the result is returned as the winning bid and its index in the original list.
Normal program (aka no privacy)
Here is the plaintext version of the program (providing no privacy) so that the auctioneer can view all of the the bids and the winning bid.
Let’s start by defining the output structure that will hold the winning bid and its index.
typedef struct Winner {
uint16_t bid;
uint16_t idx;
} Winner;
We then define the auction function, which loops through the bids in order and finds the highest one.
void auction(
uint16_t *bids,
uint16_t len,
Winner *winningBid
) {
// The first bid is the initial winner
winningBid->bid = bids[0];
winningBid->idx = 0;
// Iterate through the remaining bids, replacing the winner if a higher bid
// is found
for (uint16_t i = 1; i < len; i++) {
bool isWinner = bids[i] >= winningBid->bid;
winningBid->bid = isWinner ? bids[i] : winningBid->bid;
winningBid->idx = isWinner ? i : winningBid->idx;
}
}
Private program walkthrough
To create a private auction, we update the function’s signature with [[clang::fhe_program]] and the inputs/outputs with [[clang::encrypted]]. And that’s it, we’re done! The program now hides all the bid values.
[[clang::fhe_program]]
void auction(
[[clang::encrypted]] uint16_t *bids,
uint16_t len,
[[clang::encrypted]] Winner *winningBid
) {
// The first bid is the initial winner
winningBid->bid = bids[0];
winningBid->idx = 0;
// Iterate through the remaining bids, replacing the winner if a higher bid
// is found
for (uint16_t i = 1; i < len; i++) {
bool isWinner = bids[i] >= winningBid->bid;
winningBid->bid = isWinner ? bids[i] : winningBid->bid;
winningBid->idx = isWinner ? i : winningBid->idx;
}
}
Running the program
If you’d like to run the program, feel free to look at the corresponding code here.
Performance
Running the program with 8 bids takes 0.630 seconds on an AWS c7a.16xlarge machine (64 cores) and 2.29 seconds on an 14 inch M2 Macbook Pro with 10 cores (6 performance, 4 efficiency).
What’s missing?
In a real-world deployment, we would likely want to use threshold FHE to implement an auction. Doing so ensures that only the winning bid is known and losing bids remaing private/hidden.
Patient health risk
Some of our most sensitive data is arguably our health-related data.
With FHE, we can protect such ultra sensitive data while still enabling machine learning models to be trained over this data or receiving predictions/analysis of our risks of developing certain diseases.
In this section, we’ll look at a toy application assessing an individual’s chance of developing heart disease based on factors such as their age, weight, alcohol consumption, and existing health conditions.
How will our algorithm work?
Our algorithm aims to assess an individual’s risk of developing cardiac disease by evaluating several health and lifestyle factors. It does this by collecting parameters such as age, weight, alcohol consumption, and existing health conditions and then increments the risk score based on the interplay between these specific parameters. For example, a smoker will have a higher risk of cardiac complications, as will an individual who has a sendentary lifestyle. This score is then returned to the individual in encrypted form, which they can decrypt and use with well known risk charts to make informed decisions about their health.
Normal program (aka no privacy)
Here is the plaintext version of the program (providing no privacy) so that the whoever is performing the risk analysis can view the individual’s age, weight, height, etc.
Let’s start defining our program to assess cardiac risk. First, we define a function to get a bit from a byte array. We will need this function to extract the individual risk factors from a packed representation of the risked factors.
inline bool get_bit(uint8_t flags, unsigned int n) {
return ((flags >> n) & 0x1);
}
Inside our function, we extract the individual risk factors using the get_bit function defined earlier. In this code we access arguments through pointers; for FHE programs, all inputs are required to be passed in by reference and hence our plaintext functions follow this convention.
With all the characteristics extracted, we can now proceed to calculate the risk score by using the following conditions and sum up the results:
uint8_t cardio(
uint8_t packed_risk_factors,
uint8_t age,
uint8_t hdl,
uint8_t weight,
uint8_t height,
uint8_t physical_activity,
uint8_t glasses_alcohol
) {
bool man = get_bit(packed_risk_factors, 0);
bool smoking = get_bit(packed_risk_factors, 1);
bool diabetic = get_bit(packed_risk_factors, 2);
bool high_bp = get_bit(packed_risk_factors, 3);
uint8_t cond1 = man && (age > 50);
uint8_t cond2 = !man && (age > 60);
uint8_t cond3 = smoking;
uint8_t cond4 = diabetic;
uint8_t cond5 = high_bp;
uint8_t cond6 = hdl < 40;
uint8_t cond7 = weight > ((uint8_t) (height - 90));
uint8_t cond8 = physical_activity < 30;
uint8_t cond9 = man && (glasses_alcohol > 3);
uint8_t cond10 = !man && (glasses_alcohol > 2);
return cond1 + cond2 + cond3 + cond4 + cond5 + cond6 + cond7 + cond8 + cond9 + cond10;
}
Private program walkthrough
To create a private program, we update the function’s signature with [[clang::fhe_program]] and the inputs/outputs with [[clang::encrypted]]. And that’s it, we’re done! The program now hides all the individual’s sensitive health data from whoever is performing the risk analysis! Only the patient can view the final result.
[[clang::fhe_program]] uint8_t cardio(
[[clang::encrypted]] uint8_t packed_risk_factors,
[[clang::encrypted]] uint8_t age,
[[clang::encrypted]] uint8_t hdl,
[[clang::encrypted]] uint8_t weight,
[[clang::encrypted]] uint8_t height,
[[clang::encrypted]] uint8_t physical_activity,
[[clang::encrypted]] uint8_t glasses_alcohol
) {
bool man = get_bit(packed_risk_factors, 0);
bool smoking = get_bit(packed_risk_factors, 1);
bool diabetic = get_bit(packed_risk_factors, 2);
bool high_bp = get_bit(packed_risk_factors, 3);
uint8_t cond1 = man && (age > 50);
uint8_t cond2 = !man && (age > 60);
uint8_t cond3 = smoking;
uint8_t cond4 = diabetic;
uint8_t cond5 = high_bp;
uint8_t cond6 = hdl < 40;
uint8_t cond7 = weight > ((uint8_t) (height - 90));
uint8_t cond8 = physical_activity < 30;
uint8_t cond9 = man && (glasses_alcohol > 3);
uint8_t cond10 = !man && (glasses_alcohol > 2);
return cond1 + cond2 + cond3 + cond4 + cond5 + cond6 + cond7 + cond8 + cond9 + cond10;
}
Running the program
If you’d like to run the program, feel free to look at the corresponding code here.
Performance
Running the program takes 0.40 seconds on an AWS c7a.16xlarge machine (64 cores) and 1.41 seconds on an 14 inch M2 Macbook Pro with 10 cores (6 performance, 4 efficiency).
What’s missing?
In a real world application, the data related to risk factors would need to be stored encrypted in an Electronic Health Record (EHR) system to enable more complicated analyses.
Random number generation
Web3 systems often lack a source of randomness, which can limit the types of applications that can be made (such as games). We can develop a pseudo random number generator (PRNG). If you know the seed it is easy to generate the sequence of numbers from the PRNG; conversely, if you observe a subset of the sequence, it is difficult to determine the seed or what the next number in the sequence will be. Hence for a PRNG algorithm to be effective, the initial seed of the PRNG should not be public knowledge.
In this example, we’ll generate a PRNG function using what is known as a Linear Feedback Shift Register (LFSR). By keeping the initial seed of the PRNG secret using FHE, we can ensure that the sequence of random numbers generated is unpredictable in end user applications.
How will our algorithm work?
A Linear Feedback Shift Register (LFSR) is a sequential circuit that shifts bits through a register while applying a linear feedback function, typically implemented using XOR operations on selected bits (taps). It generates pseudo-random sequences by cycling through states determined by its initial seed and feedback configuration, providing a deterministic yet seemingly random output. The randomness arises from the mathematical properties of the feedback function, which maximizes the period of the sequence before repeating, provided the taps are chosen correctly.
Here we will generate the step to go from one random number to the next in the sequence; in practice, a program would implement this algorithm in a loop to generate a sequence of random numbers.
Normal program (aka no privacy)
One of the simplest forms of a PRNG that is highly efficient is the XORShift algorithm. This involves XORing the current state with a shifted version of itself several times. In particular, we use the 16-bit “798” Xorshift due to its long period (65535 elements) and reasonable randomness statistics. The 798 refers to the shifts used in the feedback function.
// Take in some state as `number`
uint16_t rng(uint16_t number)
{
number ^= number << 7;
number ^= number >> 9;
number ^= number << 8;
return number;
}
Private program walkthrough
To transform the prior program into a private one operating over encrypted data, we update the function’s signature with [[clang::fhe_program]] and the inputs/outputs with [[clang::encrypted]]. That’s it, we’re done! The program now hides the initial number used as the input along with the output.
[[clang::fhe_program]]
uint16_t rng([[clang::encrypted]] uint16_t number)
{
number ^= number << 7;
number ^= number >> 9;
number ^= number << 8;
return number;
}
Running the program
If you’d like to run the program, feel free to look at the corresponding code here.
Performance
Running the program takes 0.004 seconds on an AWS c7a.16xlarge machine (64 cores) and 0.009 seconds on an 14 inch M2 Macbook Pro with 10 cores (6 performance, 4 efficiency). This particular program can use very primitive FHE operations and therefore has a very fast runtime.
What’s missing?
In a real world application, the PRNG algorithm would have to be initialized with a random seed. In addition, the PRNG function would be called repeatedly to generate a sequence of pseudorandom numbers.
FAQ
This is an evolving list based on the questions we receive :)
How do I use Parasol in web3?
While Parasol can be used in web3, we have a web3-specific offering we’ve developed called the secure processing framework (SPF). SPF makes use of Parasol under-the-hood and will offer you a much better experience as a dApp developer.
Can I use Parasol with threshold TFHE?
Yes, you can. However, if you’re using threshold FHE you’ll likely want a corresponding service that responds to decryption requests and checks access control; these services will be provided as part of our secure processing framework.
Can Parasol be used with different FHE schemes?
Yes, but it requires quite a bit of work on the backend for our team. Parasol today uses our variant of the TFHE scheme. TFHE offers developers access to a wide variety of operations (compared to the BFV or CKKS fully homomorphic encryption schemes) as well as unbounded computation, making it highly suitable for a wide variety of use cases.
I’m not getting good performance when running programs. Why?!
This may be due to one (or even all) of the following reasons:
- Check you’re running in release mode (not debug mode).
- You may be running the program on a machine with insufficient cores. Our TFHE scheme variant shines if you have sufficient computing resources; a rough heuristic is you want to run the program on a machine that has as many cores as input bits (e.g. if you want to add two 16-bit integers together, you need ~32 cores).
- While program runtime may be fast, key generation for our TFHE variant is fairly expensive (i.e. many seconds to even minutes depending on the machine). You should serialize the generated keys to disk and cache them.
Sunscreen’s variant of Torus FHE
Feel free to skip this section unless you’d like to understand more about our TFHE variant.
Regardless of which FHE scheme you choose to work with today, a major challenge is something called “noise.” We won’t go into exactly what this is but it suffices to say noise is a bad thing. FHE ciphertexts have noise, and this noise grows as we perform operations. In working with FHE, we need to make sure that the noise doesn’t grow so large that we will no longer be able to successfully decrypt the message.
To reduce the noise in a ciphertext so that we can keep computing over it, FHE introduces a special operation called bootstrapping
There are various FHE schemes out there such as BFV (which Sunscreen’s prior compiler was based on), CKKS, and TFHE. The “T” in TFHE stands for torus and this scheme is sometimes referred to as CGGI16 after its authors and the year in which it was published. What’s great about TFHE is that it made bootstrapping and comparisons relatively cheap (i.e. fast) compared to other FHE schemes. For applications where it’s unclear at setup time how many computations or what kind of computations the developer wants to perform over the data, TFHE makes a lot of sense. There are some drawbacks to this scheme; most notably, arithmetic is usually more expensive using TFHE than with BFV or CKKS. Additionally, there’s a fairly noticeable performance hit when upping the precision of numeric data types (integers, floats, etc) in TFHE.
A brief history on the evolution of bootstrapping in TFHE
It turns out that there are actually a few bootstrapping varieties for TFHE; namely gate bootstrapping, functional/programmable bootstrapping, and circuit bootstrapping.
Gate bootstrapping is what most TFHE libraries and compilers rely upon. It’s a technique designed to reduce the noise in a ciphertext and comes from the original TFHE paper.
Functional (sometimes known as programmable) bootstrapping is a newer type of bootstrapping that (1) reduces the noise in a ciphertext and (2) performs a computation over the ciphertext at the same time, using the same techiques as gate bootstrapping but with different parameters.
Circuit bootstrapping was introduced many years back but appears to be used thus far for either “leveled” computations (i.e. computations of a certain circuit depth) or as an optimization when implementing certain forms of functional/programmable bootstrapping. However, it has the nice property of having an output that’s directly compatible with a (homomorphic) multiplexer.
Let’s look at how we might combine circuit bootstrapping with multiplexers to unlock performance improvements.
Breaking down our approach
We can realize arbitrary computation using multiplexers. The FHE equivalent of a multiplexer is called a “cmux.”
Our high level goal is to perform general computation using a multiplexer tree before going on to reduce the noise (via the circuit bootstrap) so that we can continue performing more computations. We must make sure we do not exceed the noise ceiling when doing the multiplexer tree, otherwise we’re in a lot of trouble. The type mismatch between the cmux and circuit bootstrap also requires us to perform some additional operations to get the output of the cmux into the “right” format to feed back into the circuit bootstrap.
We refer to our computing approach as the CBS-CMUX approach, as the combination of the two operations allows us to realize arbitrary programs. In terms of the CBS implementation itself, we implement the version described in this paper.
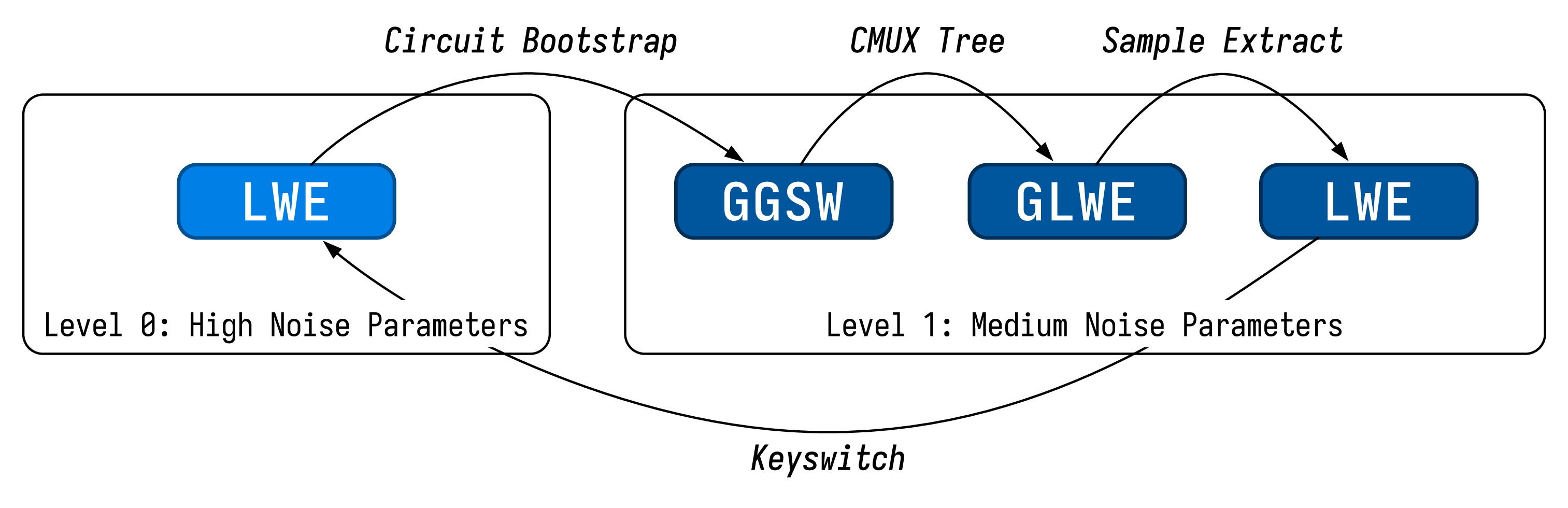
While all of this may sound very difficult to manage, our compiler handles all of this on your behalf automatically.
Why do this?
So far, all of this sounds very theoretical. What does all this effort actually buy us? Why would anyone want to use the CBS-CMUX approach?
We take a long-term view on FHE. For FHE to scale over the coming years, FHE must be architected to best suit hardware (be it cores, GPUs, or eventually ASICs), rather than expecting hardware to magically accelerate FHE.
Separately, a lot of benchmarking done thus far in FHE focuses on the performance of individual operations (e.g. a multiplication takes xx ms, an addition takes yy ms). We believe this is the wrong way of thinking about FHE; what’s important is how expensive an actual program is.
As a simple thought experiment, consider the following: In System A, each operation takes 1 second. In System B, each operation takes 2 seconds. To instantiate program P with System A, we will need 3 operations but these must be done sequentially. With System B, we also need 3 operations but these can be done all in parallel. Would you prefer to use System A or B for the program?
Our approach:
- Reduces the number of bootstrapping operations in the critical path: Specifically, for key operations like 16-bit homomorphic comparisons, our approach reduces the number of bootstraps in the critical path down to 1. This is important because bootstrapping is one of the most expensive operations in TFHE. When we instantiate a 16-bit homomorphic comparison using functional/programmable bootstrapping, there are 3 respective bootstrapping operations in the critical path. Even if we have specialized hardware, we would have to wait for each one of these functional bootstrapping operations to be done sequentially.
- Provides greater intra-circuit parallelism: When gives access to sufficient cores/computing resources, we can speed things up significantly.
But what about threshold FHE?!
Currently, we’re discussing FHE with respect to “single key” FHE, meaning one party holds onto the private key.
Don’t worry though—everything mentioned so far serves as the foundation of our threshold FHE construction. Our TFHE variant can be transformed into a threshold FHE scheme so that we can enable applications over multiple user’s data. In fact, our Parasol compiler is immediately compatible with our threshold TFHE scheme :)
Performance comparisons
We’ve benchmarked our FHE compiler against existing state-of-the-art (that support comparisons over encrypted data).
Of the 5 compilers we consider, ours is the only one to rely on circuit bootstrapping as the primary bootstrapping method. Concrete relies on programmable/functional bootstrapping whereas Google, E3, and Cingulata rely on the older gate bootstrapping approach.
We consider a variety of programs that showcase comparisons over encryped data, arithmetic operations over encrypted data, etc.
Experiments were performed on an AWS c7a.16xlarge instance (64 vCPUs, 128GB RAM). Using Lattice Estimator, we estimate that our compiler and Concrete should provide 128 bits of security. Google’s transpiler and Cingulata provide 118 bits of security, whereas E3 provides approximately 94 bits of security.
Transparently, our approach shines when sufficient cores are provided with which we can parallelize tasks across. You will see less of a performance benefit with our compiler/approach if the FHE computation is being carried out on a machine with relatively few cores (e.g. 16, 32 cores). We see a significant speed up in performance time as we go from 1 thread to 64 for the below programs. Please note that this only applies to the computing party, there’s no issue at all of the end-user (providing data) uses a laptop!
Chi-squared benchmarks
We look at how our compiler performs for a FHE-friendly variant of chi-squared test with respect to runtime of the generated FHE program, size of the compiler output, and memory usage.
| Compiler | Runtime | Program size | Memory usage |
|---|---|---|---|
| Parasol | 521ms | 232B | 365MB |
| Concrete | 5.29s | 1.41kB | 1.82GB |
| Google Transpiler | 13.8s | 323kB | 299MB |
| E3-TFHE | 440s | 2.87MB | 182MB |
| Cingulata-TFHE | 85.6s | 579kB | 254MB |
For Concrete (which determines precision based on developer-provided example inputs), we pass in 8-bit inputs to maintain the same output precision as all the other compilers.
Cardio benchmarks
We also consider how our compiler performs for the cardio program with respect to runtime of the generated FHE programs, size of the compiler output, and memory usage.
| Compiler | Runtime | Program size | Memory usage |
|---|---|---|---|
| Parasol | 409ms | 472B | 399MB |
| Concrete | 2.13s | 10.4kB | 4.0GB |
| Google Transpiler | 3.26s | 11.4kB | 274MB |
| E3-TFHE | 119s | 1.87MB | 181MB |
| Cingulata-TFHE | 2.98s | 613kB | 254MB |
For Concrete, we don’t restriction precision as the output is a small integer anyway.
Scaling results
Next, we consider how the FHE compilers scale as we vary the number of inputs.
Auction benchmarks
We consider how FHE compilers perform on a first-price sealed-bid auction as we vary the number of bids.
For our work, please note that we can obtain significantly better times when we hand-code the auction using our variant of the TFHE scheme. Nevertheless, we still observe that Parasol performs best here against all other FHE compilers.
| 2 bids | 4 bids | 8 bids | 16 bids | 32 bids | |
|---|---|---|---|---|---|
| Parasol | 0.098s | 0.275s | 0.625s | 1.315s | 2.714s |
| Concrete | 24.1s | 86.4s | 264s | 694s | 1690s |
| Google Transpiler | 2.36s | 6.72s | 15.4s | 33.1s | 68.2s |
| E3-TFHE | 12.4s | 36.6s | 84.8s | 182s | 379s |
| Cingulata-TFHE | 1.48s | 4.33s | 10.3s | 22.4s | 47.2s |
We use 16-bit precision which signficantly slows down the auction times for everyone. For Concrete, we pass in 16-bit example inputs to maintain the same input precision as the other works.
WASM
We support compiling to WASM targets though the standard WASM target backend. This is most useful for adding the ability to encrypt values in the browser using a public key, while the FHE computation runs on the server with more compute resources.
cargo build --release --target wasm32-unknown-unknown
Please see the Rust WASM documentation for more information.