Sunscreen’s variant of Torus FHE

Feel free to skip this section unless you’d like to understand more about our TFHE variant.

Regardless of which FHE scheme you choose to work with today, a major challenge is something called “noise.” We won’t go into exactly what this is but it suffices to say noise is a bad thing. FHE ciphertexts have noise, and this noise grows as we perform operations. In working with FHE, we need to make sure that the noise doesn’t grow so large that we will no longer be able to successfully decrypt the message.

To reduce the noise in a ciphertext so that we can keep computing over it, FHE introduces a special operation called bootstrapping

There are various FHE schemes out there such as BFV (which Sunscreen’s prior compiler was based on), CKKS, and TFHE. The “T” in TFHE stands for torus and this scheme is sometimes referred to as CGGI16 after its authors and the year in which it was published. What’s great about TFHE is that it made bootstrapping and comparisons relatively cheap (i.e. fast) compared to other FHE schemes. For applications where it’s unclear at setup time how many computations or what kind of computations the developer wants to perform over the data, TFHE makes a lot of sense. There are some drawbacks to this scheme; most notably, arithmetic is usually more expensive using TFHE than with BFV or CKKS. Additionally, there’s a fairly noticeable performance hit when upping the precision of numeric data types (integers, floats, etc) in TFHE.

A brief history on the evolution of bootstrapping in TFHE

It turns out that there are actually a few bootstrapping varieties for TFHE; namely gate bootstrapping, functional/programmable bootstrapping, and circuit bootstrapping.

Gate bootstrapping is what most TFHE libraries and compilers rely upon. It’s a technique designed to reduce the noise in a ciphertext and comes from the original TFHE paper.

Functional (sometimes known as programmable) bootstrapping is a newer type of bootstrapping that (1) reduces the noise in a ciphertext and (2) performs a computation over the ciphertext at the same time, using the same techiques as gate bootstrapping but with different parameters.

Circuit bootstrapping was introduced many years back but appears to be used thus far for either “leveled” computations (i.e. computations of a certain circuit depth) or as an optimization when implementing certain forms of functional/programmable bootstrapping. However, it has the nice property of having an output that’s directly compatible with a (homomorphic) multiplexer.

Let’s look at how we might combine circuit bootstrapping with multiplexers to unlock performance improvements.

Breaking down our approach

We can realize arbitrary computation using multiplexers. The FHE equivalent of a multiplexer is called a “cmux.”

Our high level goal is to perform general computation using a multiplexer tree before going on to reduce the noise (via the circuit bootstrap) so that we can continue performing more computations. We must make sure we do not exceed the noise ceiling when doing the multiplexer tree, otherwise we’re in a lot of trouble. The type mismatch between the cmux and circuit bootstrap also requires us to perform some additional operations to get the output of the cmux into the “right” format to feed back into the circuit bootstrap.

We refer to our computing approach as the CBS-CMUX approach, as the combination of the two operations allows us to realize arbitrary programs. In terms of the CBS implementation itself, we implement the version described in this paper.

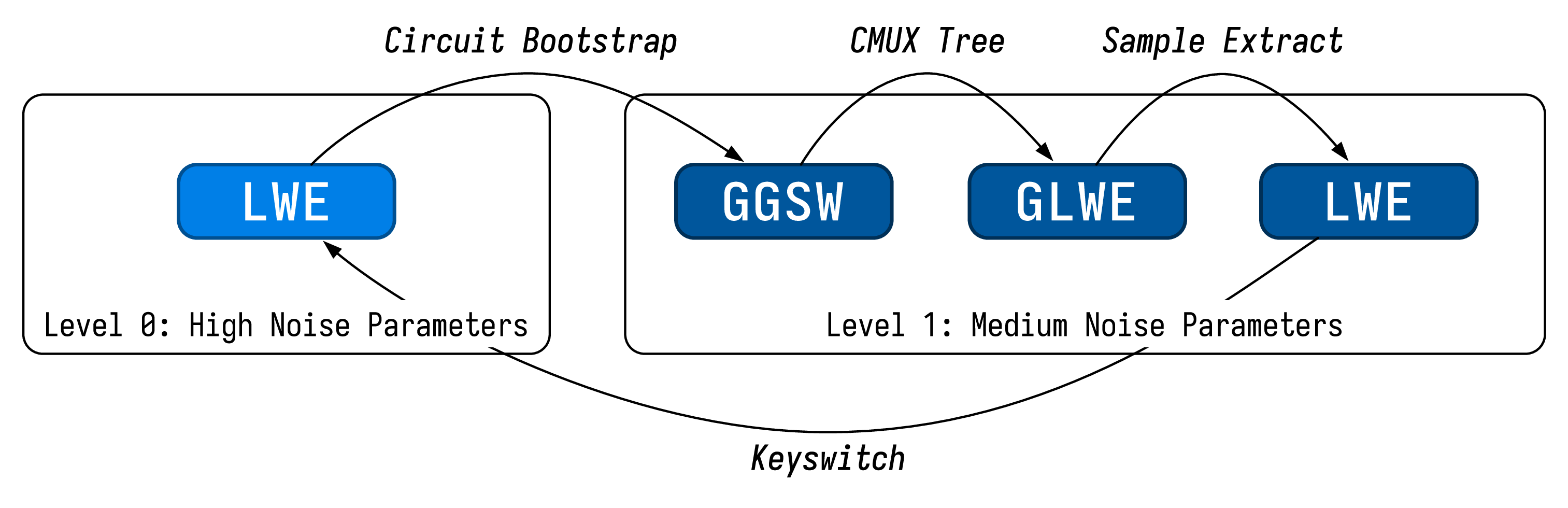
While all of this may sound very difficult to manage, our compiler handles all of this on your behalf automatically.

Why do this?

So far, all of this sounds very theoretical. What does all this effort actually buy us? Why would anyone want to use the CBS-CMUX approach?

We take a long-term view on FHE. For FHE to scale over the coming years, FHE must be architected to best suit hardware (be it cores, GPUs, or eventually ASICs), rather than expecting hardware to magically accelerate FHE.

Separately, a lot of benchmarking done thus far in FHE focuses on the performance of individual operations (e.g. a multiplication takes xx ms, an addition takes yy ms). We believe this is the wrong way of thinking about FHE; what’s important is how expensive an actual program is.

As a simple thought experiment, consider the following: In System A, each operation takes 1 second. In System B, each operation takes 2 seconds. To instantiate program P with System A, we will need 3 operations but these must be done sequentially. With System B, we also need 3 operations but these can be done all in parallel. Would you prefer to use System A or B for the program?

Our approach:

• Reduces the number of bootstrapping operations in the critical path: Specifically, for key operations like 16-bit homomorphic comparisons, our approach reduces the number of bootstraps in the critical path down to 1. This is important because bootstrapping is one of the most expensive operations in TFHE. When we instantiate a 16-bit homomorphic comparison using functional/programmable bootstrapping, there are 3 respective bootstrapping operations in the critical path. Even if we have specialized hardware, we would have to wait for each one of these functional bootstrapping operations to be done sequentially.
• Provides greater intra-circuit parallelism: When gives access to sufficient cores/computing resources, we can speed things up significantly.

But what about threshold FHE?!

Currently, we’re discussing FHE with respect to “single key” FHE, meaning one party holds onto the private key.

Don’t worry though—everything mentioned so far serves as the foundation of our threshold FHE construction. Our TFHE variant can be transformed into a threshold FHE scheme so that we can enable applications over multiple user’s data. In fact, our Parasol compiler is immediately compatible with our threshold TFHE scheme :)